この春学期中参加していた大学のとある研究プロジェクトにおいて,「コミュニケーション」を定量的に計測してやろうと思い色々やっていたのでその経緯と展望をまとめておく.
プロジェクト概要
この研究プロジェクトは簡単に言うと体育の授業で「コミュニケーションの促進」と「キャンパスの地理的理解の促進」という二つの目的を軸に設計されたゲーム形式の授業を導入しようというものである.でもって生徒全員にウォッチデバイスを着け.そこから全員の運動データを計測し,解析を行う.まだ実際に体育の授業に導入してはおらず(倫理審査とか色々あって大変らしい),研究室内で行った少人数での実験データのみが取れている状況で,その少ないデータを使って何か春学期中に僕が貢献できることはないかと考えた結果,ゲーム内でのコミュニケーションを定量的に計測するというテーマに行き着いた訳である.ゲーム内でどれだけコミュニケーションが取れているかが分かればこのプロジェクトの目的である「コミュニケーションの促進」に対する評価指標として用いることができる.データとしては各被験者について座標データと速度データが時系列で取れているのでこれらを使ってどうにか定量的な計測を試みた.
コミュニケーションの定義
一般的にコミュニケーションというのはいささか主観的で,何をすればコミュニケーションなのか,話せば良いのか,会釈も含まれるのかなど厳密に定義をするのは難しい.そこで今回は,「各被験者の座標がある程度近づいてお互いがある程度近い範囲で視野に入っている」状態をコミュニケーションと定義した.ある程度が多すぎてこれだけではいまいち伝わらないだろうが,大まかに以下の流れでコミュニケーションの回数を計測する.
- 前準備として2種類の時系列データ(座標データと速度データ)の抜け落ちを補間する
- 座標データから進行方向を計算する
- 速度データから視野角を推定する
- 視野角と進行方向から各被験者の各タイムスタンプにおける「コミュニケーション可能範囲」を推定する
- 同じタイムスタンプにおいて2人の被験者がお互いの「コミュニケーション可能範囲」に入っていればコミュニケーションとし,この回数を計測する
座標データ,速度データの補間
ゲーム中,被験者のウォッチデバイスで計測される運動データは随時UDPでサーバーに送信されている.しかしパケロスやサーバーの処理落ちなどによりデータが抜け落ちることがある.実際予備実験で得たデータもかなり抜け落ちがあり,多い部分では4分ほど連続して抜け落ちていた.これではデータの解析ができないので,抜け落ちたデータを補間する必要がある.今回は単純に2種類のデータに対して線形補間を行った.以下にある被験者の座標データの補間結果を示す.
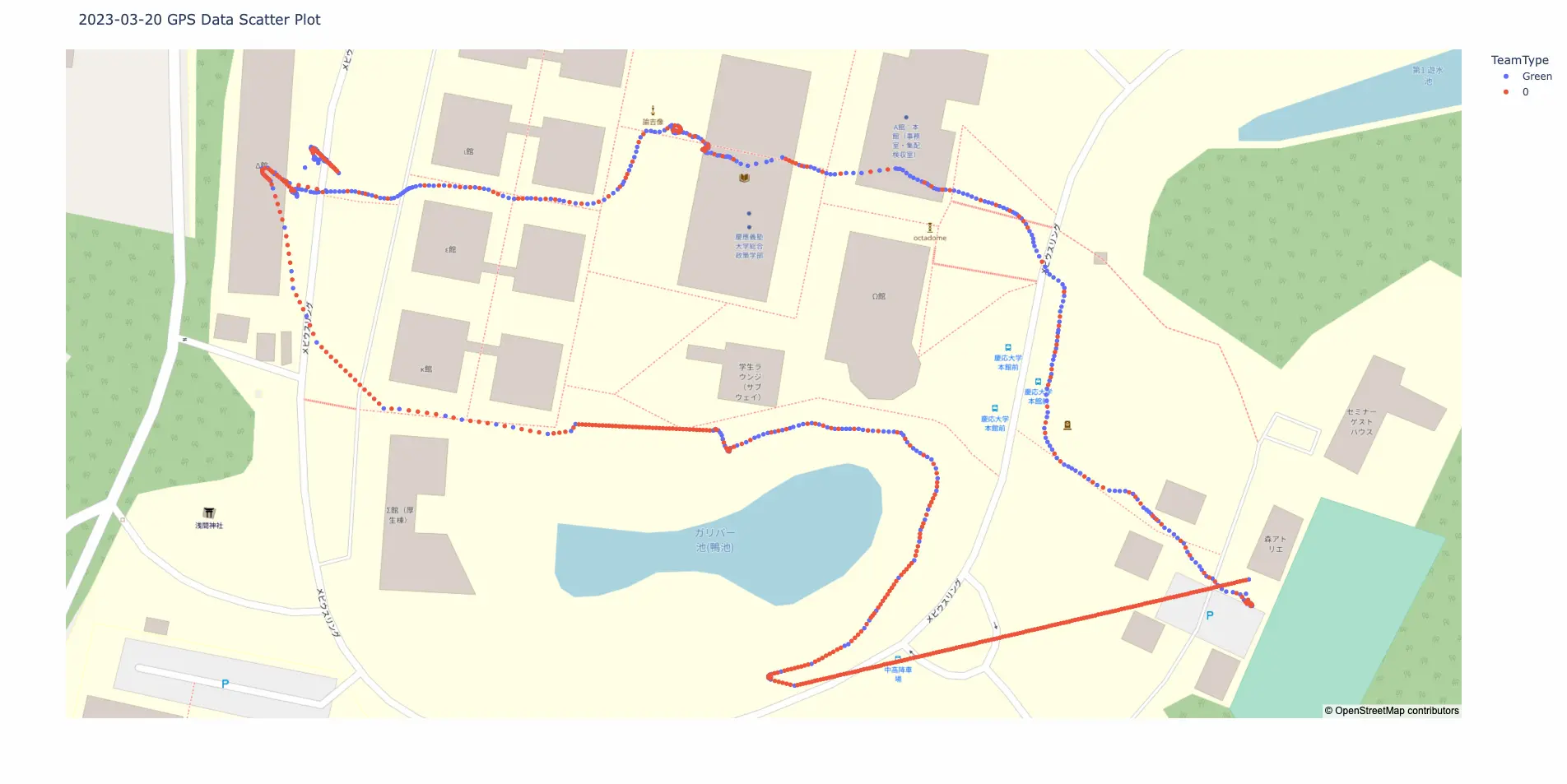
青い点が元データで,赤い点が補間されたデータである.基本的には自然に補完できているが,南東部分の補間はものすごく線形になっている.これは元データがおよそ4分ほど抜けていた部分で,ここに関しては線形補間以外のアルゴリズムを使っても同じような不自然さにはなる気がする.
進行方向の計算
補間を行い連続した座標の値が得られたので次はこの時系列データを用いて各被験者の進行方向を計算する.方法は至ってシンプルで,連続したタイムスタンプの座標データを結んだ直線の方位角を求めるだけである.
def calculate_bearing(lat1, lon1, lat2, lon2):
lon_diff = np.radians(lon2 - lon1)
lat1, lon1, lat2, lon2 = map(np.radians, (lat1, lon1, lat2, lon2))
x = np.sin(lon_diff) * np.cos(lat2)
y = np.cos(lat1) * np.sin(lat2) - (np.sin(lat1) * np.cos(lat2) * np.cos(lon_diff))
initial_bearing = np.arctan2(x, y)
initial_bearing = np.degrees(initial_bearing)
compass_bearing = (initial_bearing + 360) % 360
return compass_bearing
これで各被験者の各タイムスタンプにおける進行方向が計算できた.
視野角の推定
座標データ同様に速度データにも補間を施し,連続した時系列データを得た.ここから視野角を推定する.PAHOの文献によると,人間の水平方向の視野角は時速40kmでは100度,時速70kmでは75度,時速100kmでは45度まで縮小するらしい.これを使って3次スプライン補間を行い,各被験者の各タイムスタンプにおける視野角を推定した.
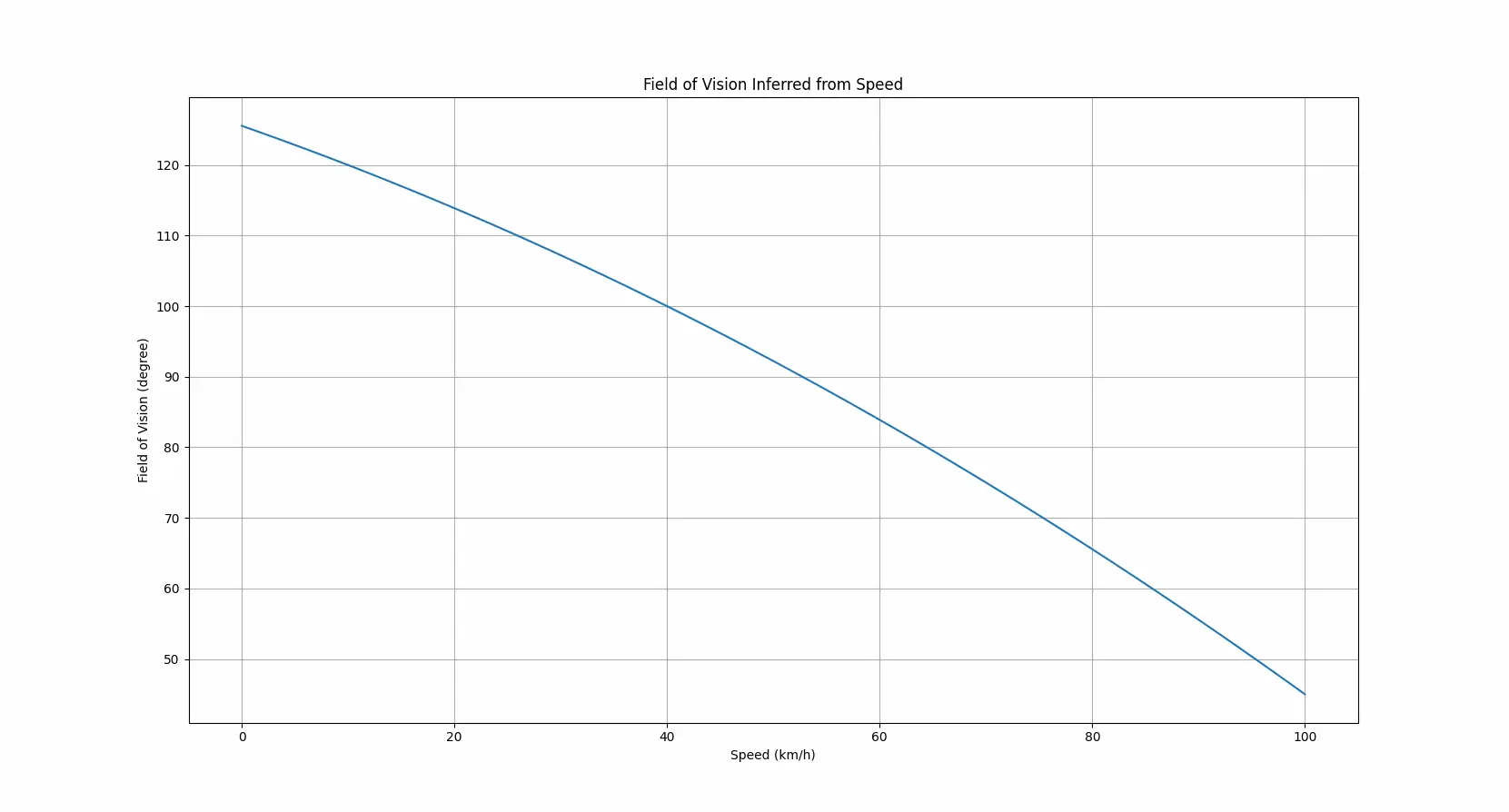
本来視野角を推定するには半径の推定も必要だが,今回は「コミュニケーション可能範囲」の推定が最終的な目的であるためここでは角度のみを推定する
コミュニケーション可能範囲の推定
推定にはとどまるが進行方向と視野角が得られたので,ここからある被験者のあるタイムスタンプでの「コミュニケーション可能範囲」を推定する.イメージとしては以下のような扇形の領域になる感じ.
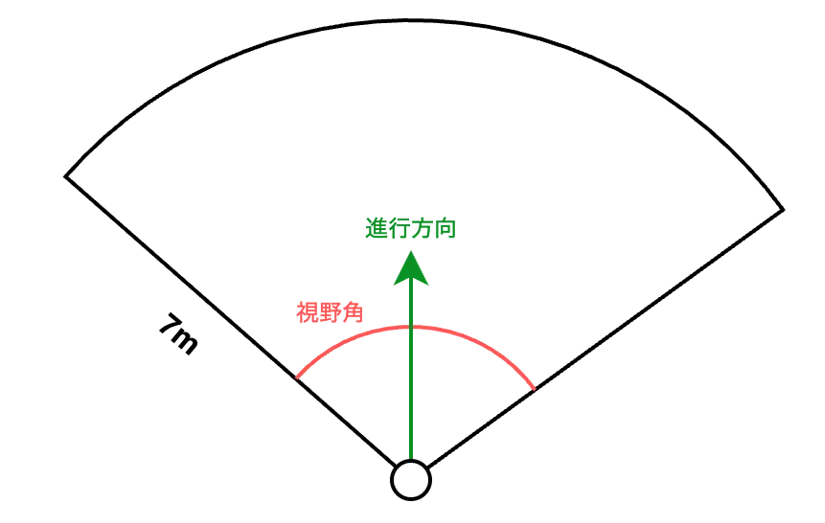
ここで半径を7mとしているのはPersonal SpaceのWikipediaの西出和彦による分類によれば3~7mの距離では知り合いを無視することはできないとされていたからである.実を言うとこれは元の文献が物理本らしく,国会図書館くらいにしかなさそうだったので実際には読んでいない.まあ1985年に出て反証が出ていないので大方認められた概念なのだろう.
排他域: 50 cm 以下.絶対的に他人を入れたくない範囲で,会話などはこんなに近づいては行わない.
会話域: 50 cm - 1.5 m.日常の会話が行われる距離である. このゾーンに入ると会話することが強制的であるような距離圧力を受ける.すなわち会話なしではいられない.もし会話がないときは何らかの「居ること」の理由を必要とする.
近接域: 1.5 - 3 m.普通,会話をするためにこのゾーンに入るが,会話をしないでこのゾーンに居続けることも不可能ではない.距離圧力としては微妙なゾーンであり,しばらく会話なしでいると居心地が悪くなる距離である.
相互認識域: 3 - 20 m.このゾーンでは,知り合いであるかどうかが分かり,相手の顔の表情も分かる.普通,挨拶が発生する距離である.特に,3 - 7 mの距離では,知り合いを無視することはできない.
本当はこのコミュニケーション範囲を地図にプロットして可視化できたらかっこよかったのだが,僕のmatplotlib力と時間の都合上断念した.
コミュニケーション回数の計測
上で推定した「コミュニケーション可能範囲」を基に,各被験者の各タイムスタンプにおいてコミュニケーションが取れているかを計測する.具体的には,あるタイムスタンプにおいて2人の被験者がお互いの「コミュニケーション可能範囲」に入っていればコミュニケーションとし,この回数を計測する.
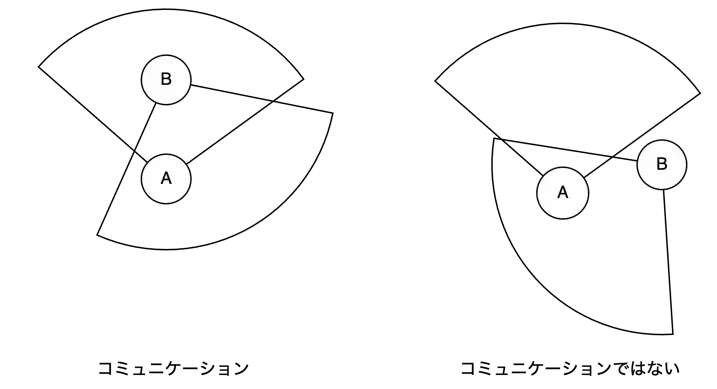
def in_field_of_view(lat1, lon1, bearing1, fov1, lat2, lon2):
distance = haversine((lat1, lon1), (lat2, lon2), unit=Unit.METERS)
if distance > 7:
return False
bearing_to_2_from_1 = bearing.calculate_bearing(lat1, lon1, lat2, lon2) min_bearing1 = (bearing1 - fov1 / 2 + 360) % 360
max_bearing1 = (bearing1 + fov1 / 2 + 360) % 360
return min_bearing1 <= bearing_to_2_from_1 <= max_bearing1
まずhaversineアルゴリズムを用いて2点間の距離を算出し,それが7m以上であれば既に範囲から外れているので処理を終了する.次に2点間の方位角を計算し,その方位角が「コミュニケーション可能範囲」の中に入っているかを判定する.この作業を2点の両方に対して行い,双方ともに「コミュニケーション可能範囲」に入っていればコミュニケーションとしてカウントする.これを全てのタイムスタンプに対して行う.タイムスタンプの数を
精度上げたい
上で述べた方法でコミュニケーション回数を計測することはできたが,実際にはまだ精度が低い.そもそもコミュニケーションというのは毎タイムスタンプごとに発生するものではなく,連続的なものである.今のアルゴリズムでは10秒の接近が10回のコミュニケーションとカウントされて無駄に回数が多くなっているので,もう少しメモリを消費して連続性を検知できるようにしたい.というかしている最中である.
あとは検定の方法も考える必要がある.そもそもプロジェクトにおいて「コミュニケーション」の定義が曖昧という問題はあるが,本番でこのアルゴリズムを使うなら何かしら信頼性がないといけない.パッと思いつく方法で言うと予備実験の時に被験者が自分でコミュニケーション回数とか相手を記録しておいて,アルゴリズムによる計測と比較するとか,アンケートで定性的なデータをとって比較するみたいなことはできそうである.
おわりに
春学期は色々なことに追われすぎて個人開発も全然進まなかった結果がこのブログの放置期間なので,夏休みは頑張るぞ.