単に円周率を使いたいなら
import math
print(math.py)
で良いんだけども,3.14がどうやって求まっているのか自分でやってみたい.
というわけで確率的モデルで円周率を求めていきたいと思います.
第一象限の適当なところに点を打っていく
まずx座標とy座標それぞれで,0から1のランダムな数値を定めて点を打ちます
import random
x, y = random.random(), random.random()
x^2+y^2が1以内かどうか確かめる
このxとyをそれぞれ2乗してお互いに足し合わせた数が1以内であれば,点は半径1の円の内側にあることになります.
number = x ** 2 + y ** 2 #これが1以内であれば円の内側
何回も繰り返して近似値を見る
これを何回も繰り返して,繰り返した数を分母,1以内だった回数×4(全ての象限で同じ結果になると仮定する)を分子とすると,円周率が算出されます.試しに1000回くらい繰り返してみましょう.
import random
incount = 0
def GenerateRandom():
x, y = random.random(), random.random()
number = x ** 2 + y ** 2
return number
iteration = 1000
for ite in range(iteration):
check = GenerateRandom()
if (check < 1):
incount += 1
quadrant = 4 #全象限
print(incount * quadrant / iteration)
3.2
うーん,微妙.数が少なかったようなので1000万回で試してみましょう.
# 5秒くらいかかります
3.141382
良きかな.
可視化してみる
数字が出ただけだとあんまり感動しなかったのでmatplotlibで可視化してみましょう.
まずは1000回バージョン
import random
import matplotlib.pyplot as plt
def GenerateRandom():
x, y = random.random(), random.random()
number = x ** 2 + y ** 2
return [number, x, y]
iteration = 1000
for ite in range(iteration):
check = GenerateRandom()
if (check[0] < 1):
plt.scatter(check[1], check[2], c = 'red', s = 10)
else:
plt.scatter(check[1], check[2], c='blue', s = 10)
plt.title('Monte Carlo Method')
plt.xlabel("x")
plt.ylabel("y")
plt.show()
10秒くらい待つと…
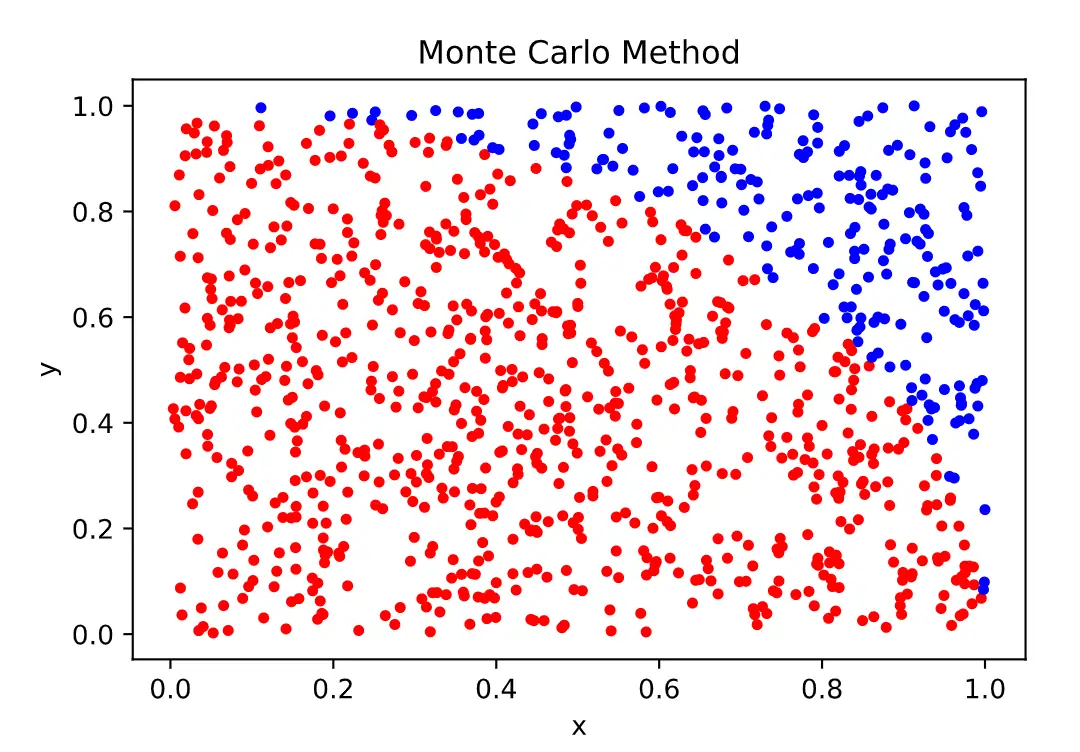
イマイチ分かりにくいので1000万回バージョンをみてみましょう.
import random
import matplotlib.pyplot as plt
def GenerateRandom():
x, y = random.random(), random.random()
number = x ** 2 + y ** 2
return [number, x, y]
iteration = 10000000
for ite in range(iteration):
check = GenerateRandom()
if (check[0] < 1):
plt.scatter(check[1], check[2], c = 'red', s = 10)
else:
plt.scatter(check[1], check[2], c='blue', s = 10)
plt.title('Monte Carlo Method')
plt.xlabel("x")
plt.ylabel("y")
plt.show()
これを実行したら一旦パソコンから離れて散歩でもしましょう.帰ってきた頃には処理が終わっているはずです.

グラフを正方形にすればより分かりやすいですが,綺麗に弧を描いて分布しているのが分かります.
これを計算したからといって何か生まれるわけでもありませんが,興味を持った方は試していただけると嬉しいです.